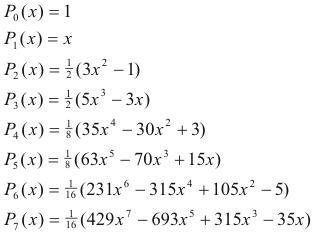Los Polinomios de Legendre: Las ‘Fórmulas Mágicas’ de la Física
Los polinomios de Legendre son una poderosa herramienta matemática que ha demostrado ser fundamental en una amplia variedad de campos científicos, desde la física teórica hasta la ingeniería y la estadística. Nombrados en honor al matemático francés Adrien-Marie Legendre, estos polinomios tienen una apariencia simple pero esconden un profundo poder que los convierte en una especie de «fórmulas mágicas» en la física y las ciencias relacionadas. En este artículo, exploraremos qué son los polinomios de Legendre, cómo se derivan y cómo se aplican en diversas áreas del conocimiento.
¿Qué son los Polinomios de Legendre?
Los polinomios de Legendre son una secuencia de funciones polinómicas ortogonales que se utilizan para resolver ecuaciones diferenciales y problemas de valores límite en la física y la matemática aplicada. Estos polinomios se definen a través de una fórmula recursiva y se denotan comúnmente como ��(�)Pn(x), donde �n es un número entero no negativo que representa el orden del polinomio.
La Fórmula Recursiva de los Polinomios de Legendre
La fórmula recursiva que define los polinomios de Legendre es la siguiente:
�0(�)=1P0(x)=1 �1(�)=�P1(x)=x ��+1(�)=(2�+1)���(�)−���−1(�)�+1Pn+1(x)=n+1(2n+1)xPn(x)−nPn−1(x)
Esta fórmula permite calcular los polinomios de Legendre de cualquier orden a partir de los polinomios de orden inferior. Comenzando con �0(�)P0(x) y �1(�)P1(x), se pueden generar todos los demás polinomios.
Propiedades de los Polinomios de Legendre
Los polinomios de Legendre tienen varias propiedades interesantes que los hacen útiles en una variedad de aplicaciones. Algunas de estas propiedades incluyen:
- Ortogonalidad: Los polinomios de Legendre son ortogonales en el intervalo [−1,1][−1,1], lo que significa que el producto de dos polinomios de Legendre diferentes integrados en este intervalo es igual a cero. Esta propiedad es esencial en problemas de valores límite y descomposición de funciones en series.
- Recurrencia: La fórmula recursiva permite calcular polinomios de orden superior a partir de los de orden inferior, lo que simplifica los cálculos en problemas complicados.
- Solución a la Ecuación de Laplace: Los polinomios de Legendre son soluciones a la ecuación de Laplace en coordenadas esféricas, lo que los hace fundamentales en problemas de potencial electrostático y gravitacional.
Aplicaciones en Física y Ciencias Relacionadas
Los polinomios de Legendre tienen una amplia gama de aplicaciones en diversas disciplinas científicas. Algunas de las áreas en las que se utilizan incluyen:
1. Mecánica Cuántica
En la mecánica cuántica, los polinomios de Legendre se utilizan para describir los orbitales atómicos y la forma de los electrones en átomos y moléculas. Estos polinomios son esenciales para comprender la estructura electrónica de la materia.
2. Cosmología
En cosmología, los polinomios de Legendre se utilizan para describir las anisotropías en el fondo cósmico de microondas, lo que proporciona información crucial sobre la estructura a gran escala del universo y su evolución a lo largo del tiempo.
3. Ingeniería
En ingeniería, estos polinomios se aplican en problemas de calor y transferencia de masa, así como en la representación de campos de radiación en antenas y en la teoría de placas y vigas.
4. Estadística
En estadística, los polinomios de Legendre se utilizan en la expansión de funciones en series de Legendre, que son fundamentales en el análisis de datos y la estimación de parámetros en modelos estadísticos.
Conclusión
Los polinomios de Legendre son una herramienta matemática poderosa y versátil que desempeña un papel fundamental en la física, la ingeniería, la estadística y otras disciplinas científicas. Su capacidad para resolver ecuaciones diferenciales, su ortogonalidad y sus propiedades matemáticas únicas los convierten en una verdadera «fórmula mágica» que ha permitido avances significativos en nuestra comprensión del mundo natural y en la resolución de problemas complejos en diversas áreas de la ciencia y la tecnología.