Introducción
Los números han fascinado a la humanidad desde tiempos inmemoriales. A lo largo de la historia, diversas culturas han atribuido significados y propiedades especiales a números particulares, y han explorado las relaciones matemáticas que existen entre ellos. Uno de estos números especiales que ha intrigado a matemáticos y entusiastas por igual son los números prónicos. En este artículo, descubriremos la magia de los números cuadrados y exploraremos las propiedades sorprendentes de los números prónicos.
¿Qué son los Números Pronicos?
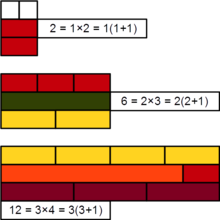
Los números prónicos son una categoría única de números enteros. Un número prónico es el producto de dos enteros consecutivos, es decir, un número de la forma «n(n+1)». Por ejemplo, 6, 12 y 20 son números prónicos, ya que se pueden expresar como 23, 34 y 4*5, respectivamente.
La Fascinación de los Números Cuadrados
Antes de sumergirnos en el mundo de los números prónicos, es importante entender la importancia de los números cuadrados en este contexto. Los números cuadrados son una clase especial de números prónicos en la que ambos factores son iguales. Por ejemplo, 4, 9 y 16 son números cuadrados, ya que son el producto de un número por sí mismo (22, 33 y 4*4).
Los números cuadrados han desempeñado un papel esencial en la historia de las matemáticas y en diversas aplicaciones prácticas. Desde las pirámides egipcias hasta las ecuaciones cuadráticas de la álgebra, los números cuadrados han sido fundamentales en la resolución de problemas complejos.
Propiedades de los Números Pronicos
Los números prónicos también tienen propiedades interesantes que los hacen dignos de estudio. Algunas de estas propiedades incluyen:
- Suma de números consecutivos: Los números prónicos pueden expresarse como la suma de números consecutivos. Por ejemplo, 30 es un número prónico (5*6) y también puede expresarse como la suma de los cinco primeros números enteros (1 + 2 + 3 + 4 + 5).
- Relación con los números triangulares: Existe una relación interesante entre los números prónicos y los números triangulares. Los números triangulares son aquellos que pueden expresarse como la suma de los primeros números naturales. Los números prónicos pueden generarse a partir de los números triangulares sumando 1 al término triangular anterior.
- Conexión con las secuencias de Fibonacci: Los números prónicos también están relacionados con la famosa secuencia de Fibonacci. Si tomamos el cociente de dos números prónicos consecutivos, obtenemos una aproximación cada vez mejor a la «proporción áurea», un número irracional misterioso que aparece en la naturaleza y el arte.
Aplicaciones de los Números Pronicos
Los números prónicos tienen aplicaciones en diversas áreas, desde las matemáticas puras hasta la ciencia y la ingeniería. Algunas de sus aplicaciones incluyen:
- Geometría: Los números prónicos están relacionados con la construcción de figuras geométricas, como triángulos y cuadrados. También se utilizan en la teoría de números para explorar las propiedades de las raíces cuadradas.
- Ingeniería: En ingeniería, los números prónicos se utilizan en el diseño de estructuras, especialmente cuando se necesita distribuir cargas de manera uniforme.
- Informática: Los números prónicos tienen aplicaciones en algoritmos y programación, especialmente en la optimización de recursos y la distribución equitativa de tareas.
Conclusión
Los números prónicos y su relación con los números cuadrados son un fascinante campo de estudio en las matemáticas. Estos números poseen propiedades únicas y tienen una amplia gama de aplicaciones prácticas. Al explorar la magia de los números cuadrados y los números prónicos, ampliamos nuestra comprensión de las matemáticas y descubrimos la belleza y la elegancia que subyace en el mundo de los números enteros.