Los Conjuntos de Cantor: Infinitos Dentro de Infinitos
Introducción
El mundo de las matemáticas es un lugar fascinante y repleto de maravillas que desafían nuestra comprensión. Uno de los conceptos más intrigantes en este ámbito es el conjunto de Cantor, una construcción matemática que revela la profunda naturaleza de los números reales y la noción de infinito. En este artículo, exploraremos los Conjuntos de Cantor y desentrañaremos su misterio, demostrando cómo dentro de lo que consideramos infinito, podemos encontrar infinitos aún más asombrosos.
I. El Conjunto de Cantor Original
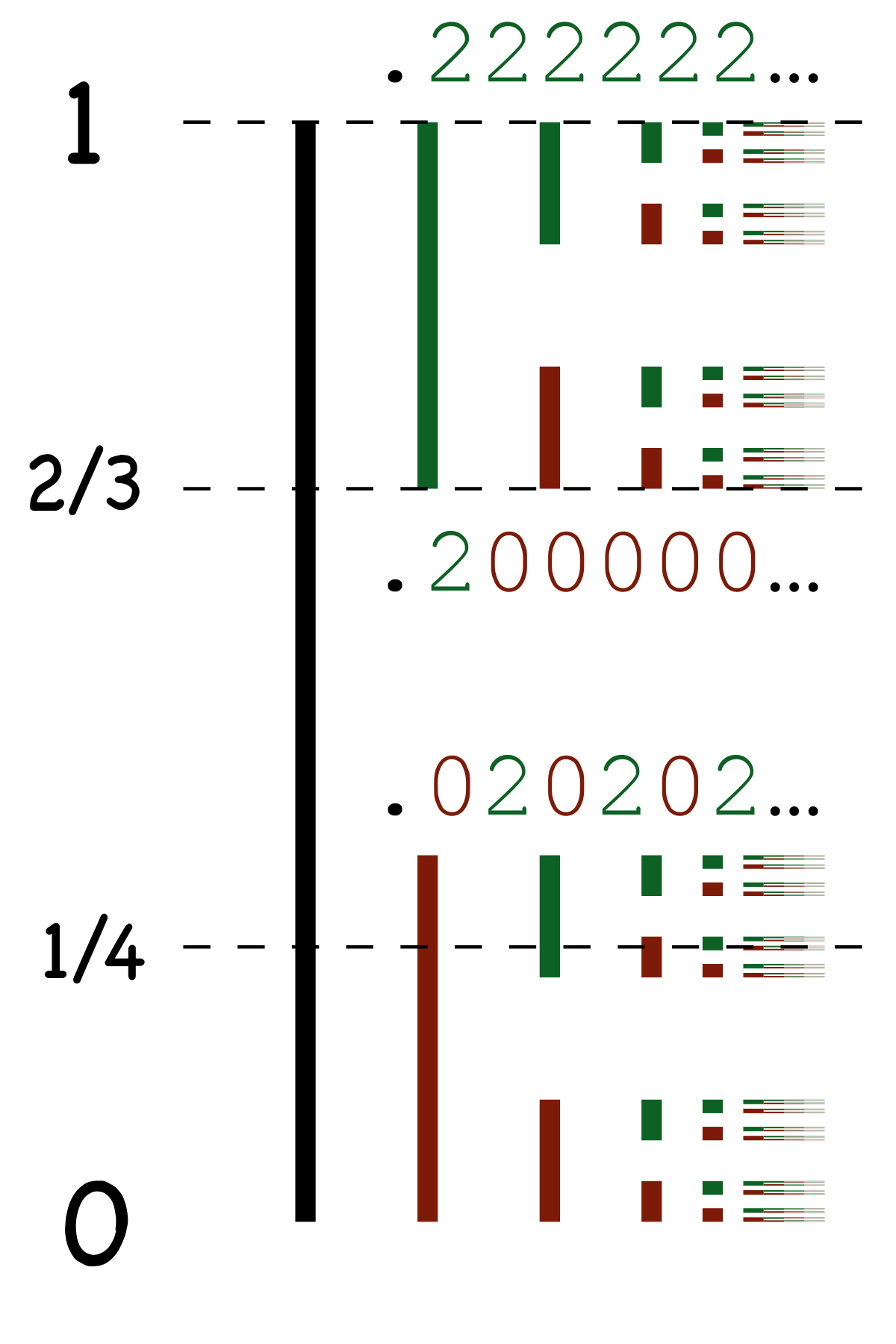
El Conjunto de Cantor, nombrado en honor al matemático alemán Georg Cantor, se originó en la segunda mitad del siglo XIX. Su construcción es ingeniosa y sencilla a la vez. Comenzamos con un segmento de línea, por ejemplo, el intervalo de números reales entre 0 y 1. Luego, procedemos a eliminar un tercio del segmento, dejando dos intervalos más pequeños. Este proceso se repite una y otra vez, infinitamente.
El resultado es un conjunto que, a simple vista, parece estar vacío, ya que no contiene ningún número real en particular. Sin embargo, aquí es donde comienza la sorprendente paradoja de los Conjuntos de Cantor.
II. Cardinalidad del Conjunto de Cantor
Uno de los conceptos más desafiantes en matemáticas es la comparación de conjuntos infinitos para determinar su «tamaño» o cardinalidad. Sorprendentemente, el Conjunto de Cantor no está vacío, a pesar de que parezca haber eliminado una cantidad infinita de elementos. Su cardinalidad es igual a la del conjunto de números reales en el intervalo de 0 a 1, es decir, es un conjunto no numerable.
Este resultado es un ejemplo claro de cómo los Conjuntos de Cantor revelan infinitos dentro de infinitos. A pesar de su apariencia inicial de vacío, este conjunto contiene una cantidad igualmente infinita de números, lo que desafía nuestra intuición sobre la naturaleza del infinito.
III. Propiedades Fascinantes
Los Conjuntos de Cantor también tienen propiedades notables. Por ejemplo, son perfectamente inmersos en sí mismos, lo que significa que si tomamos una porción cualquiera del conjunto, esa porción es topológicamente idéntica al conjunto completo. Esto es una rareza en el mundo de los conjuntos y refuerza la idea de que los Conjuntos de Cantor son realmente infinitos en su esencia.
IV. Generalizaciones y Aplicaciones
A lo largo de los años, los Conjuntos de Cantor han dado lugar a numerosas generalizaciones y extensiones matemáticas. Los matemáticos han explorado variantes de este conjunto en diferentes dimensiones y han aplicado sus propiedades en diversos campos de las matemáticas, como la teoría de la medida y la topología.
Además, los Conjuntos de Cantor también tienen aplicaciones en la teoría de números y la teoría de fractales. Su estudio ha permitido a los matemáticos profundizar en la comprensión de la estructura de los números reales y ha dado lugar a la creación de conceptos matemáticos innovadores.
Conclusión
Los Conjuntos de Cantor son una joya en el mundo de las matemáticas, que desafía nuestras intuiciones sobre el infinito y nos muestra cómo dentro de lo que consideramos infinito, existen niveles aún más profundos de infinitud. A través de su construcción y propiedades, los Conjuntos de Cantor nos invitan a explorar los misterios de los números reales y nos muestran la belleza de las estructuras matemáticas que subyacen en nuestro universo. En última instancia, estos conjuntos nos recuerdan que las matemáticas son un viaje interminable hacia la comprensión de nuestro mundo y más allá.