La Paradoja de Zeno: ¿Cómo Puede Aquiles Atravesar la Tortuga?
La Paradoja de Zeno es un fascinante problema filosófico que ha desconcertado a mentes brillantes durante siglos. Este enigma, planteado por el antiguo filósofo griego Zenón de Elea en el siglo V a.C., se centra en una situación aparentemente absurda: ¿cómo puede el rápido Aquiles alcanzar y superar a una tortuga que tiene una ventaja inicial?
La Paradoja de Zeno: Un Dilema que Desafía la Lógica
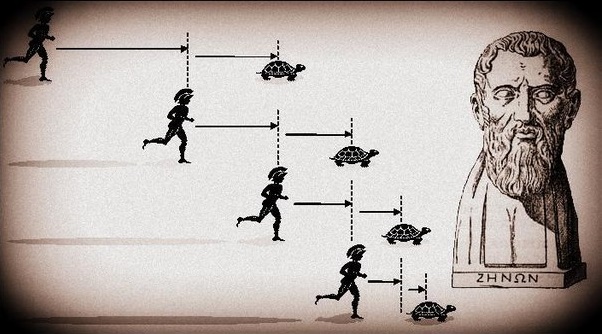
Zenón argumentaba que, para que Aquiles alcance a la tortuga, primero debe llegar al punto donde la tortuga comenzó su carrera. Pero mientras Aquiles recorre esa distancia, la tortuga avanza un pequeño trecho. Cuando Aquiles llega a ese nuevo punto, la tortuga se ha movido nuevamente. Este proceso parece repetirse infinitamente, lo que lleva a la conclusión de que Aquiles nunca alcanzará realmente a la tortuga.
El Mito de Aquiles y la Tortuga
La paradoja de Zeno se ilustra de manera efectiva mediante el famoso mito de Aquiles y la tortuga. Imaginemos que Aquiles da a la tortuga una ventaja inicial de, digamos, 10 metros en una carrera. Aquiles es extremadamente rápido y puede correr 10 veces más rápido que la tortuga, pero según el razonamiento de Zenón, siempre habrá una brecha entre ellos.
Para calcular cuánto tiempo tomará a Aquiles alcanzar a la tortuga, primero debe recorrer los 10 metros iniciales. Sin embargo, durante ese tiempo, la tortuga ha avanzado un metro adicional. Ahora, Aquiles debe recorrer ese metro extra, pero durante ese tiempo, la tortuga ha avanzado otro metro. Este proceso parece no tener fin, lo que sugiere que Aquiles nunca logrará superar a la tortuga.
Resolviendo la Paradoja de Zeno
Aunque la Paradoja de Zeno parece desafiar la lógica, en realidad tiene una solución que se basa en conceptos matemáticos y el infinito. El truco radica en el reconocimiento de que la serie de distancias que Aquiles debe recorrer se reduce cada vez más. Si sumamos 10 metros, luego 1 metro, luego 0.1 metros y así sucesivamente, obtenemos una serie infinita convergente que tiene una suma finita.
En otras palabras, aunque hay una cantidad infinita de distancias que Aquiles debe recorrer para alcanzar a la tortuga, la suma total de estas distancias es finita y, por lo tanto, Aquiles eventualmente alcanzará a la tortuga. Esto se basa en los principios matemáticos del cálculo infinitesimal, que fueron desarrollados mucho después de la época de Zenón.
La Importancia Filosófica y Matemática
La Paradoja de Zeno ha sido un punto de discusión en la filosofía y las matemáticas durante siglos. Si bien la resolución matemática es clara, la paradoja plantea preguntas profundas sobre la naturaleza del tiempo, el espacio y el infinito. ¿Son estas ideas realmente tan incomprensibles como parecen?
En última instancia, la Paradoja de Zeno nos recuerda la capacidad de la mente humana para plantear preguntas desafiantes y encontrar soluciones incluso en los problemas más enigmáticos. Aunque Zenón pudo haber intentado demostrar que el movimiento y el cambio son ilusiones, la resolución de esta paradoja ha demostrado que la lógica y las matemáticas pueden superar incluso los enigmas más intrincados de la filosofía antigua.
En conclusión, la Paradoja de Zeno plantea una pregunta fascinante sobre la relación entre el infinito y la realidad, y aunque inicialmente puede parecer desconcertante, una comprensión matemática adecuada nos muestra que Aquiles puede, de hecho, alcanzar a la tortuga. Esta paradoja perdura como un recordatorio de la intersección entre la filosofía y las matemáticas, y cómo juntas pueden arrojar luz sobre los misterios más profundos de la existencia.