La Paradoja de Monty Hall: El Dilema de Elegir Puertas
Introducción
La Paradoja de Monty Hall es un enigma que ha desconcertado a matemáticos, estadísticos y entusiastas de los juegos de azar durante décadas. Nombrada en honor al presentador de televisión Monty Hall, este problema ilustra de manera sorprendente la importancia de la probabilidad en la toma de decisiones. A pesar de su aparente simplicidad, el dilema de elegir puertas ha generado un debate feroz y ha demostrado que la intuición humana en ocasiones puede conducir a resultados sorprendentes y contraintuitivos.
El Escenario
Imaginemos que te encuentras en un programa de televisión. Frente a ti hay tres puertas, detrás de una de ellas se encuentra un premio valioso, como un automóvil, y detrás de las otras dos puertas hay cabras. Inicialmente, no sabes qué hay detrás de cada puerta.
El Dilema
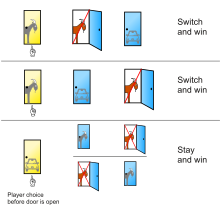
Comienzas eligiendo una de las tres puertas, digamos la número 1. Luego, el presentador, Monty Hall, quien conoce el contenido detrás de cada puerta, abre una de las dos puertas restantes que no has seleccionado, revelando una cabra. Ahora, te enfrentas a un dilema: ¿debes mantener tu elección inicial (la puerta número 1) o cambiar a la otra puerta que no ha sido abierta por Monty (la puerta número 2 o 3)?
La Intuición Errónea
La intuición inicial de la mayoría de las personas es que no importa si cambian su elección o no. Después de todo, hay dos puertas restantes, y la probabilidad de que el premio esté detrás de cualquiera de ellas debería ser del 50%, ¿verdad? Sin embargo, aquí es donde entra en juego la sorprendente paradoja.
La Solución Contraintuitiva
La respuesta correcta es que deberías cambiar tu elección. La probabilidad de ganar el premio aumenta significativamente si decides cambiar de puerta después de que Monty Hall revele una cabra detrás de una de las dos puertas no seleccionadas inicialmente. Para entender por qué, consideremos las dos posibilidades:
- Manteniendo tu elección inicial:
- Probabilidad de ganar: 1/3
- Probabilidad de perder: 2/3
- Cambiando tu elección después de que Monty revela una cabra:
- Probabilidad de ganar: 2/3
- Probabilidad de perder: 1/3
La clave de esta paradoja radica en el momento en que Monty revela una cabra. Al hacerlo, efectivamente te proporciona información adicional, aumentando las probabilidades a tu favor si decides cambiar. Aunque pueda parecer contraintuitivo, los números no mienten: cambiar de puerta duplica tus posibilidades de ganar.
La Explicación Matemática
La Paradoja de Monty Hall se puede explicar de manera matemática mediante la teoría de la probabilidad condicional. Cuando Monty revela una cabra, condiciona la información que tienes. Las probabilidades se redistribuyen y, en última instancia, cambiar de puerta se convierte en la estrategia más favorable.
Conclusión
La Paradoja de Monty Hall, a pesar de su simplicidad aparente, ilustra de manera poderosa cómo la intuición humana puede llevarnos por el camino equivocado en situaciones probabilísticas. Al comprender la matemática detrás de este dilema, podemos aprender valiosas lecciones sobre la toma de decisiones informadas y la importancia de la probabilidad en la vida cotidiana. La próxima vez que te enfrentes a una elección difícil, recuerda la lección de Monty Hall y considera si cambiar de puerta podría ser la mejor estrategia para alcanzar tus objetivos.