La Cuadratura del Círculo: Un Enigma Matemático que Desafió a los Antiguos
Introducción
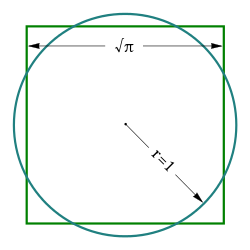
La Cuadratura del Círculo es un enigma matemático que ha intrigado a la humanidad durante siglos. Esta problemática se centra en un desafío aparentemente imposible: ¿Es posible construir un cuadrado que tenga la misma área que un círculo dado utilizando únicamente una regla y un compás? A lo largo de la historia, grandes matemáticos y pensadores se han enfrentado a esta pregunta, buscando una solución que parecía escapar a las capacidades de las herramientas matemáticas disponibles en su época.
Los Primeros Intentos
Los antiguos griegos fueron los pioneros en la exploración de la Cuadratura del Círculo. Uno de los primeros en abordar este desafío fue Anaxágoras, quien vivió en el siglo V a.C. Aunque no logró resolver el problema, sus esfuerzos iniciaron una tradición de investigación que se prolongaría durante siglos.
Arquímedes y su Aproximación
El matemático griego Arquímedes, quien vivió en el siglo III a.C., realizó importantes avances en la Cuadratura del Círculo. Si bien no logró una solución exacta, desarrolló un método para calcular el valor de π (pi) con una precisión sorprendente utilizando un enfoque de aproximación. Utilizando polígonos inscritos y circunscritos al círculo, Arquímedes demostró que π estaba comprendido entre 3 1/7 y 3 10/71, acercándose significativamente al valor actual de π.
Los Problemas de la Cuadratura del Círculo
A medida que la matemática avanzaba, los matemáticos se daban cuenta de que la Cuadratura del Círculo presentaba desafíos fundamentales. En el siglo XIX, el matemático alemán Ferdinand von Lindemann demostró de manera concluyente que era imposible resolver este problema utilizando únicamente una regla y un compás. Su demostración se basó en la trascendencia de π, lo que significa que π es un número irracional y no puede ser expresado como una raíz cuadrada.
Avances Modernos
Aunque la Cuadratura del Círculo resultó ser un problema insoluble con las restricciones originales, la matemática moderna ha encontrado soluciones alternativas y aproximaciones útiles. Por ejemplo, el cálculo integral permite calcular el área bajo una curva, incluyendo el área de un círculo, de manera precisa. Además, el desarrollo de la geometría no euclidiana en el siglo XIX amplió la comprensión de las formas y las métricas, lo que permitió a los matemáticos explorar nuevos enfoques para la Cuadratura del Círculo.
Conclusión
La Cuadratura del Círculo ha sido un enigma matemático fascinante que ha desafiado a los pensadores a lo largo de la historia. Aunque los antiguos griegos y matemáticos posteriores realizaron valiosos esfuerzos para resolver este problema, la demostración de la imposibilidad de Lindemann puso fin a la búsqueda de una solución exacta. Sin embargo, el enigma persiste como un ejemplo de cómo los desafíos aparentemente imposibles pueden inspirar la exploración matemática y llevar al desarrollo de nuevas ramas de las matemáticas. La Cuadratura del Círculo sigue siendo un recordatorio de la capacidad humana para perseguir incansablemente la comprensión en el mundo de las matemáticas.