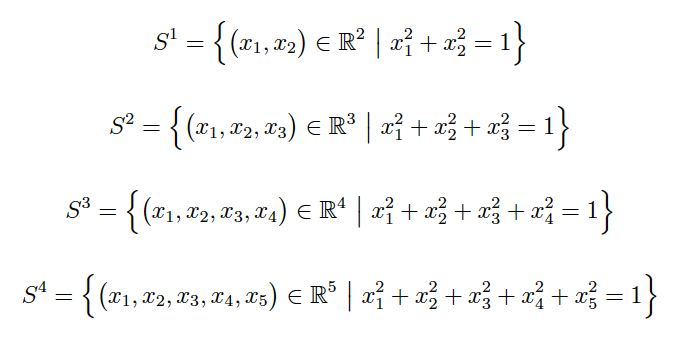La Conjetura de Poincaré: Un Problema Resuelto por Grigori Perelman
Introducción
La Conjetura de Poincaré ha sido durante mucho tiempo uno de los enigmas más desafiantes en el campo de las matemáticas. Formulada por el matemático francés Henri Poincaré a principios del siglo XX, esta conjetura se convirtió en un problema fascinante que resistió los intentos de resolución durante décadas. Sin embargo, en el año 2003, un matemático ruso llamado Grigori Perelman logró resolver este misterio que desconcertó a generaciones de matemáticos. En este artículo, exploraremos la historia de la Conjetura de Poincaré, los antecedentes de Grigori Perelman y los detalles de su sorprendente solución.
I. La Conjetura de Poincaré
La Conjetura de Poincaré se originó en el campo de la topología, una rama de las matemáticas que se ocupa del estudio de las propiedades espaciales que se mantienen constantes bajo deformaciones continuas. Formulada por primera vez por Henri Poincaré en 1904, la conjetura planteaba una pregunta fundamental sobre la esfera tridimensional: ¿Es toda variedad simplemente conexa homeomorfa a una esfera tridimensional? En otras palabras, la conjetura preguntaba si cualquier objeto tridimensional sin agujeros o «asas» era esencialmente igual a una esfera.
II. Los Intentos Previos de Resolución
La Conjetura de Poincaré se convirtió en uno de los problemas más intrigantes y desafiantes de las matemáticas, y atrajo a numerosos matemáticos que intentaron resolverla a lo largo del siglo XX. Varias aproximaciones y teoremas parciales se desarrollaron en el proceso, pero nadie pudo ofrecer una prueba completa y definitiva de la conjetura.
III. Grigori Perelman: El Matemático en la Sombra
Grigori Perelman nació en Leningrado, Rusia, en 1966, y desde temprana edad demostró una habilidad excepcional en las matemáticas. Sin embargo, su camino hacia la fama en el mundo de las matemáticas estuvo lleno de obstáculos y desafíos. Se graduó de la Universidad Estatal de San Petersburgo y obtuvo un Ph.D. en matemáticas. A lo largo de su carrera, Perelman trabajó en diversos campos matemáticos, pero fue su enfoque en la geometría riemanniana y la topología lo que finalmente lo llevó a abordar la Conjetura de Poincaré.
IV. La Solución Revolucionaria
En 2003, Grigori Perelman publicó una serie de artículos en línea que presentaban su solución a la Conjetura de Poincaré. Su enfoque se basó en la teoría de las variedades Ricci y las ecuaciones de Ricci, que se utilizan en la geometría riemanniana. Perelman desarrolló un método revolucionario para abordar la conjetura, que implicaba el uso de la métrica de Ricci y la topología de la variedad en cuestión. Su trabajo fue exhaustivo y meticuloso, y finalmente proporcionó una prueba completa de la conjetura que dejó perplejos a muchos matemáticos.
V. La Controversia y el Reconocimiento
La publicación en línea de Perelman de su solución a la Conjetura de Poincaré desencadenó una controversia en la comunidad matemática. A pesar de la solidez de su prueba, Perelman se retiró de la escena matemática y rechazó varios premios y reconocimientos, incluyendo la Medalla Fields, la máxima distinción en matemáticas. Su retiro y su renuncia a la fama fueron objeto de debate y discusión, pero su solución a la conjetura finalmente fue aceptada y reconocida por la comunidad matemática internacional.
VI. Legado y Significado
La resolución de la Conjetura de Poincaré por Grigori Perelman tuvo un impacto profundo en el campo de las matemáticas. Su trabajo abrió nuevas puertas en la topología y la geometría riemanniana, y su enfoque innovador ha influido en muchas áreas de investigación matemática. Aunque Perelman eligió retirarse de la vida pública, su legado perdura como uno de los logros más significativos en la historia de las matemáticas.
Conclusión
La Conjetura de Poincaré, un problema matemático que desconcertó a los mejores mentes durante más de un siglo, finalmente encontró su resolución en manos de Grigori Perelman, un matemático ruso recluso y genio solitario. Su solución revolucionaria y su elección de retirarse de la fama hicieron de Perelman una figura enigmática en el mundo de las matemáticas. La resolución de la conjetura dejó una marca indeleble en la historia de las matemáticas y continúa inspirando a las generaciones futuras de matemáticos a abordar desafíos aparentemente insuperables en busca de soluciones innovadoras.