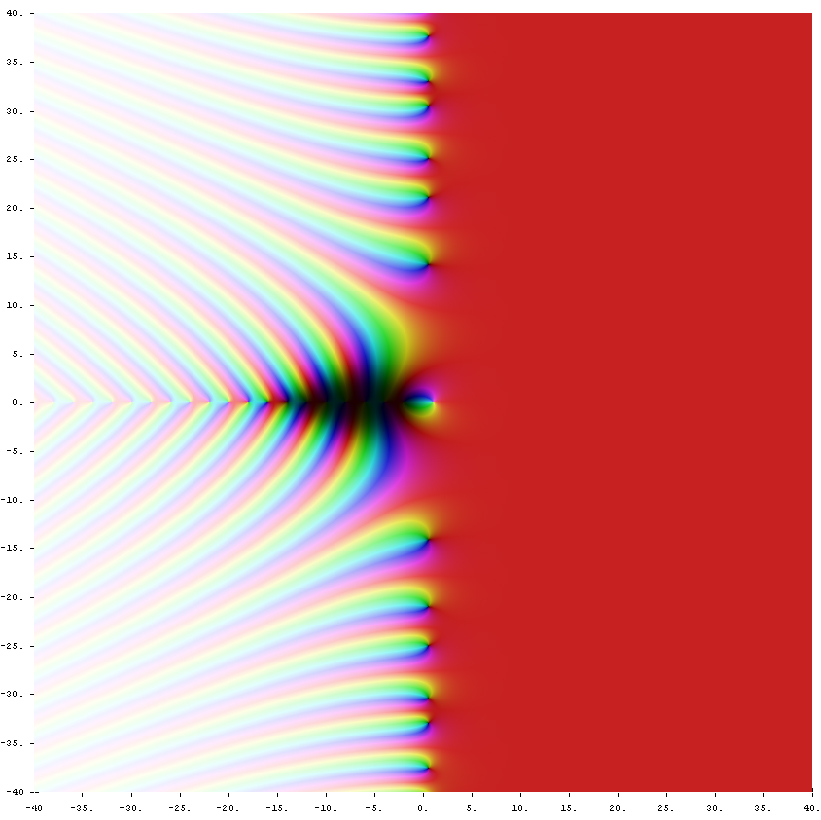
La Función Zeta de Riemann: Conexiones Entre Números Primos y el Caos
La Función Zeta de Riemann es una de las joyas más brillantes y enigmáticas de las matemáticas. Su historia está entrelazada con la teoría de números y la física teórica, y ha sido objeto de fascinación y estudio durante más de un siglo. En este artículo, exploraremos la Función Zeta de Riemann y su sorprendente conexión con los números primos y el caos en el mundo de las matemáticas y la física.
¿Qué es la Función Zeta de Riemann?
La Función Zeta de Riemann, denotada comúnmente como ζ(s), es una función matemática que desempeña un papel esencial en la teoría de números. Fue introducida por el matemático suizo Leonhard Euler en el siglo XVIII, pero fue el matemático alemán Bernhard Riemann quien la llevó a nuevas alturas en el siglo XIX. La función está definida para números complejos s, lo que la hace especialmente intrigante y poderosa.
La forma más simple de definir ζ(s) es a través de la siguiente serie infinita:
ζ(s) = 1^(-s) + 2^(-s) + 3^(-s) + 4^(-s) + …
Sin embargo, esta definición solo es válida para valores de s donde la serie converge. La Función Zeta de Riemann se extiende de manera analítica a todo el plano complejo, excepto para un punto especial en s = 1, donde tiene una singularidad.
La Hipótesis de Riemann y los Números Primos
Uno de los problemas más famosos y no resueltos en las matemáticas es la Hipótesis de Riemann, formulada por Bernhard Riemann en 1859. Esta hipótesis establece que todos los ceros no triviales (es decir, aquellos que no son simples consecuencias de la función gamma) de la Función Zeta de Riemann tienen una parte real igual a 1/2.
Aunque la Hipótesis de Riemann es un enigma no resuelto, su importancia radica en su conexión con la distribución de los números primos. El matemático alemán Carl Friedrich Gauss observó inicialmente patrones intrigantes en la distribución de los números primos, y Riemann se dio cuenta de que la Función Zeta de Riemann podría proporcionar respuestas a estas preguntas.
La Función Zeta de Riemann se relaciona con la distribución de los números primos a través de una fórmula llamada la Fórmula de Euler de Productos Infinitos. Esta fórmula expresa ζ(s) como un producto infinito sobre todos los números primos:
ζ(s) = 1/(2^(s-1)) * (pi^(s/2)) * (s-1)! * Π(p/(p^s-1))
Donde Π denota el producto sobre todos los números primos (p) y la fórmula es válida para valores de s donde la serie converge. Esta conexión entre la Función Zeta de Riemann y los números primos ha llevado a importantes avances en la teoría de números y ha sido una fuente constante de investigación y especulación.
Caos y la Función Zeta de Riemann
Más allá de su importancia en la teoría de números, la Función Zeta de Riemann también ha demostrado ser relevante en la física teórica, específicamente en el estudio del caos cuántico. El caos cuántico se refiere a la complejidad y la impredecibilidad en sistemas cuánticos, y la Función Zeta de Riemann ha surgido en el contexto de este fenómeno.
La conexión entre la Función Zeta de Riemann y el caos cuántico se basa en la relación entre los ceros no triviales de ζ(s) y los niveles de energía de sistemas cuánticos. A través de la Teoría de Cuerdas y otras herramientas matemáticas, los físicos han descubierto que los ceros de ζ(s) están relacionados con la distribución de los niveles de energía en sistemas cuánticos complejos.
Esta inesperada conexión entre la teoría de números y la física cuántica ha generado una emocionante área de investigación conocida como «la física de la Función Zeta de Riemann». Los científicos están explorando cómo los patrones de los ceros de ζ(s) pueden proporcionar información sobre la naturaleza del caos cuántico y las propiedades fundamentales del universo.
Conclusión
La Función Zeta de Riemann es un objeto matemático extraordinario que ha capturado la imaginación de matemáticos y físicos durante generaciones. Su misteriosa relación con los números primos y su sorprendente conexión con el caos cuántico son testigos de la profunda interconexión entre diferentes ramas del conocimiento humano.
Aunque la Hipótesis de Riemann sigue siendo un desafío sin resolver, la Función Zeta de Riemann continúa siendo un faro de conocimiento y un recordatorio de que, en el mundo de las matemáticas y la física, siempre hay más preguntas por descubrir y respuestas por revelar.