La Geometría Proyectiva: Cuando las Líneas Paralelas se Encuentran en el Infinito
La geometría es una disciplina fascinante que ha evolucionado a lo largo de la historia, desde los antiguos matemáticos griegos hasta los desarrollos más modernos en el campo de la geometría diferencial. Uno de los aspectos más intrigantes de la geometría es la forma en que modela y representa el espacio y las relaciones entre objetos en ese espacio. En este artículo, exploraremos un enfoque especial de la geometría conocido como «Geometría Proyectiva», que ofrece una perspectiva única sobre la relación entre las líneas paralelas y el concepto del infinito.
Los Fundamentos de la Geometría Proyectiva
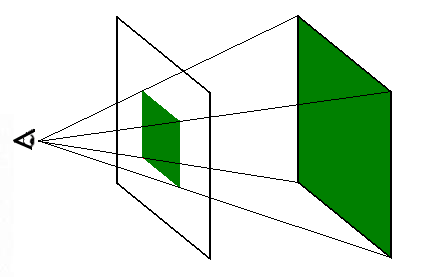
La Geometría Proyectiva es una rama de la geometría que se centra en las propiedades y las relaciones geométricas que se mantienen inalteradas bajo proyecciones y transformaciones proyectivas. A diferencia de la geometría euclidiana tradicional, en la que las líneas paralelas nunca se cruzan, la geometría proyectiva abraza la idea de que las líneas paralelas se encuentran en un punto en el infinito. Este concepto puede parecer sorprendente a primera vista, pero es fundamental para comprender cómo funciona la geometría proyectiva.
El Punto del Infinito
En la geometría proyectiva, se introduce un elemento especial llamado «punto del infinito» o «punto imposible». Este punto se considera el lugar donde todas las líneas paralelas se intersectan. Es importante destacar que el punto del infinito no se encuentra en el espacio tridimensional en el que vivimos, sino que es una construcción abstracta que se utiliza para extender la geometría más allá de sus límites convencionales.
Transformaciones Proyectivas
Una de las características distintivas de la geometría proyectiva es su enfoque en las transformaciones proyectivas. Estas transformaciones son proyecciones o mapeos que conservan las propiedades geométricas esenciales, como la incidencia y la colinealidad. Las transformaciones proyectivas pueden llevar líneas rectas a líneas rectas y mantienen el punto del infinito inalterado.
Aplicaciones de la Geometría Proyectiva
La geometría proyectiva tiene una amplia gama de aplicaciones en diversas disciplinas, desde la geometría descriptiva utilizada en la representación gráfica hasta la visión por computadora y la geometría algebraica. En la visión por computadora, por ejemplo, la geometría proyectiva se utiliza para calibrar cámaras y realizar reconstrucciones tridimensionales a partir de imágenes bidimensionales.
El Teorema de Desargues
Uno de los resultados más importantes de la geometría proyectiva es el Teorema de Desargues, que establece condiciones bajo las cuales dos triángulos están en perspectiva desde un punto. Este teorema es fundamental en la geometría proyectiva y tiene numerosas aplicaciones en la geometría euclidiana y en la resolución de problemas geométricos.
Conclusión
La Geometría Proyectiva es una rama fascinante de las matemáticas que desafía nuestras intuiciones geométricas convencionales. Al permitir que las líneas paralelas se encuentren en el infinito, esta disciplina nos ofrece una perspectiva única sobre el espacio y las transformaciones geométricas. A lo largo de la historia, la geometría proyectiva ha demostrado ser invaluable en una variedad de aplicaciones, desde la representación gráfica hasta la visión por computadora. Al explorar el mundo de la geometría proyectiva, nos sumergimos en un reino de conceptos abstractos que amplían nuestra comprensión del espacio y la forma.