La Paradoja del Cumpleaños: Probabilidad en las Fechas de Nacimiento
Introducción
La Paradoja del Cumpleaños es uno de los problemas de probabilidad más fascinantes y sorprendentes que existen. A pesar de que pueda parecer un mero juego de números, esta paradoja desafía nuestra intuición y nos muestra cómo la probabilidad puede operar de manera inesperada en situaciones cotidianas. En este artículo, exploraremos en detalle esta intrigante paradoja, desglosando sus fundamentos matemáticos y ofreciendo ejemplos para ayudar a comprenderla mejor.
¿Qué es la Paradoja del Cumpleaños?
La Paradoja del Cumpleaños plantea la siguiente pregunta: ¿Cuál es la probabilidad de que al menos dos personas en un grupo compartan la misma fecha de cumpleaños? A primera vista, podríamos pensar que esta probabilidad es relativamente baja, ya que existen 365 días en un año. Sin embargo, la realidad es sorprendentemente diferente.
El Experimento Mental
Para comprender mejor esta paradoja, consideremos un experimento mental en el que tenemos un grupo de personas. Comenzamos preguntándole a la primera persona cuál es su fecha de cumpleaños, y hay 365 posibilidades diferentes. Cuando preguntamos a la segunda persona, todavía hay 365 posibilidades diferentes para su cumpleaños, independientemente de la respuesta de la primera persona. Así sucesivamente, a medida que preguntamos a más personas, la cantidad de combinaciones posibles aumenta rápidamente.
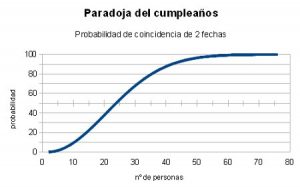
El Resultado Sorprendente
La paradoja se torna asombrosa cuando calculamos la probabilidad de que NO haya coincidencia de cumpleaños en el grupo y luego restamos ese valor de 1 para obtener la probabilidad de que SÍ haya coincidencia. Sorprendentemente, descubrimos que en un grupo de tan solo 23 personas, la probabilidad de que al menos dos de ellas compartan el mismo cumpleaños es superior al 50%. Este resultado desafía la intuición, ya que esperaríamos que se necesitara un grupo mucho más grande para que esto ocurriera.
Fundamentos Matemáticos
Para comprender los fundamentos matemáticos de esta paradoja, podemos utilizar el concepto de probabilidad complementaria. La probabilidad de que no haya coincidencia de cumpleaños en un grupo de n personas se puede calcular multiplicando las probabilidades de que cada persona tenga un cumpleaños diferente al de las demás. Esto se expresa como:
P(No coincidencia) = (365/365) * (364/365) * (363/365) * … * ((365 – n + 1)/365)
Luego, para encontrar la probabilidad de que SÍ haya coincidencia, simplemente restamos este valor de 1:
P(Coincidencia) = 1 – P(No coincidencia)
El resultado es la probabilidad de que al menos dos personas compartan el mismo cumpleaños en el grupo.
Conclusiones
La Paradoja del Cumpleaños es un ejemplo fascinante de cómo la probabilidad puede ser contraintuitiva en situaciones cotidianas. Aunque pueda parecer sorprendente, en grupos relativamente pequeños, la probabilidad de que al menos dos personas compartan el mismo cumpleaños es sorprendentemente alta. Esta paradoja no solo es un desafío interesante para nuestra intuición, sino que también tiene aplicaciones prácticas en campos como la criptografía y la planificación de eventos. En resumen, la próxima vez que celebres un cumpleaños en un grupo, recuerda la Paradoja del Cumpleaños y sorprende a tus amigos con tus conocimientos sobre probabilidad.