La Constante Matemática ‘e’: El Número Base de la Exponenciación
Introducción
En el vasto universo de las matemáticas, hay un número que destaca por su importancia y omnipresencia en una multitud de aplicaciones: la constante matemática ‘e’. Este número, aproximadamente igual a 2.71828, es el protagonista de numerosas ecuaciones y conceptos en matemáticas y ciencias. A lo largo de este artículo, exploraremos en profundidad qué es la constante ‘e’, su historia, propiedades matemáticas y sus aplicaciones en diversos campos.
Historia de ‘e’
La historia de la constante ‘e’ se remonta al siglo XVII, cuando el matemático escocés John Napier introdujo por primera vez el concepto de logaritmos. Napier observó que existía una relación entre las progresiones aritméticas y geométricas, lo que llevó a la idea de los logaritmos, que simplificaban cálculos multiplicativos complejos en adiciones simples. Sin embargo, ‘e’ como lo conocemos hoy en día fue definido y nombrado por el matemático suizo Leonhard Euler en el siglo XVIII. Euler investigó las propiedades de esta constante mientras estudiaba problemas de interés compuesto y crecimiento exponencial.
¿Qué es ‘e’?
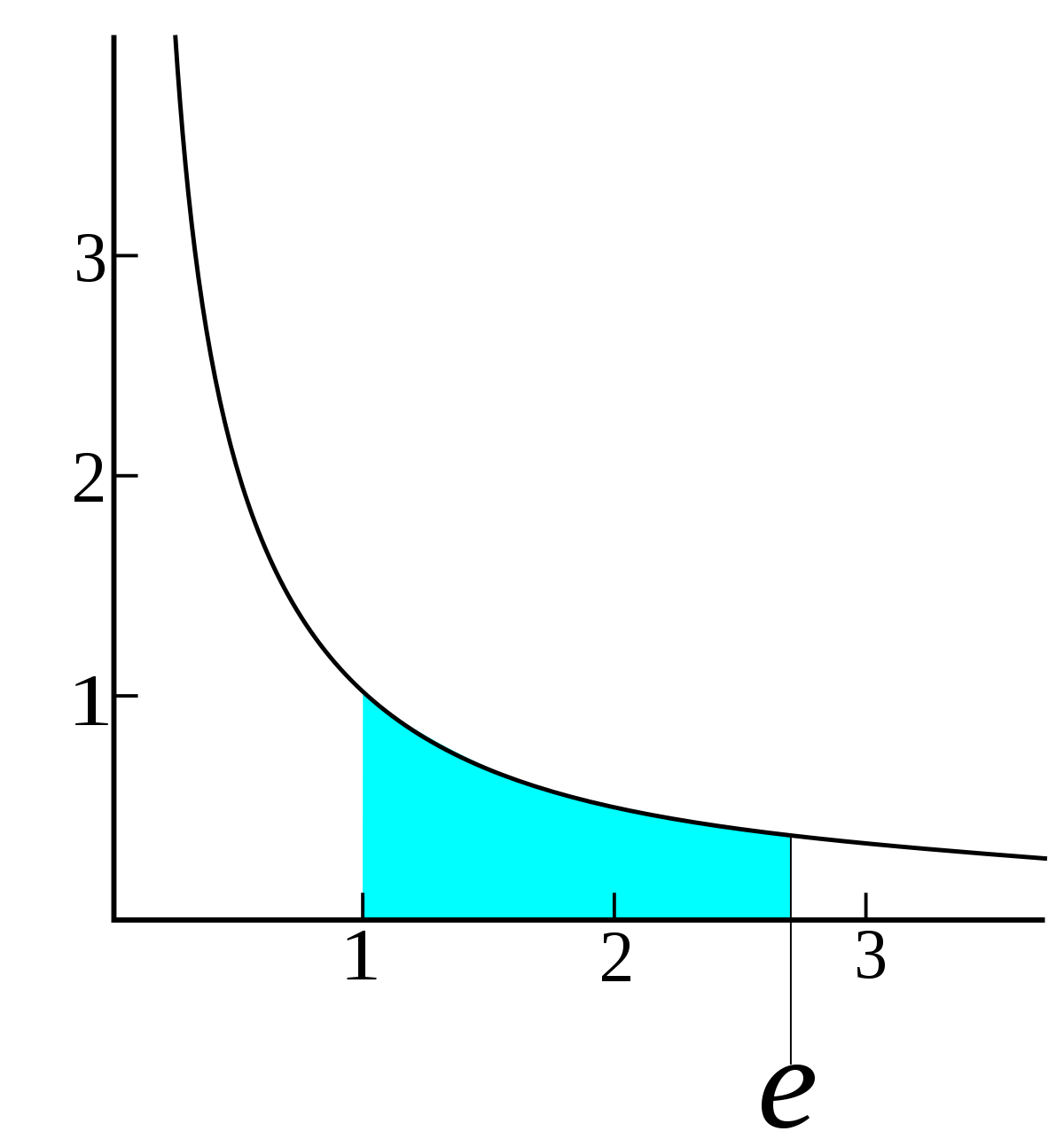
La constante ‘e’ es el número irracional que resulta de la suma infinita de la serie infinita 1 + 1/1 + 1/2 + 1/6 + 1/24 + 1/120 + … y se representa matemáticamente como:
�=1+11+12+16+124+1120+…e=1+11+21+61+241+1201+…
Una de las propiedades más fascinantes de ‘e’ es que es la única constante que, cuando se deriva, devuelve el mismo valor. Es decir, la derivada de ��ex es ��ex. Esto hace que ‘e’ sea fundamental en el estudio de las funciones exponenciales y logarítmicas.
Aplicaciones en Matemáticas
La constante ‘e’ se encuentra en el corazón de diversas ramas de las matemáticas. Algunas de sus aplicaciones más notables incluyen:
- Funciones Exponenciales: La función exponencial ��ex es fundamental en cálculo y análisis matemático. Aparece en la modelización de crecimiento poblacional, decaimiento radioactivo y fenómenos naturales como la ley de enfriamiento de Newton.
- Cálculo Diferencial: ‘e’ es esencial en cálculo diferencial y ecuaciones diferenciales. La fórmula de Euler para la identidad trigonométrica ���=cos(�)+�sin(�)eix=cos(x)+isin(x) es una joya matemática que relaciona las funciones exponenciales complejas y trigonométricas.
- Probabilidad y Estadística: La distribución exponencial, que describe el tiempo entre eventos en un proceso de Poisson, utiliza ‘e’ como base. Además, ‘e’ se relaciona con el valor esperado en probabilidad, lo que es fundamental en estadísticas.
Aplicaciones en Ciencias Naturales
La constante ‘e’ también desempeña un papel crucial en diversas disciplinas científicas, incluyendo la física y la biología. Algunos ejemplos notables son:
- Física: ‘e’ aparece en las leyes de la termodinámica, especialmente en la ley de enfriamiento de Newton y la ley de decaimiento radiactivo. Además, es fundamental en la teoría de la relatividad de Einstein y en la mecánica cuántica.
- Biología: En biología, ‘e’ se utiliza para modelar el crecimiento exponencial de poblaciones y la cinética de reacciones químicas enzimáticas.
Conclusiones
La constante matemática ‘e’ es uno de los pilares fundamentales de las matemáticas y las ciencias naturales. Su omnipresencia en una amplia gama de aplicaciones la convierte en una de las constantes más importantes en la historia de las matemáticas. Desde su humilde origen en el siglo XVII hasta su prominencia en la era moderna de la ciencia, ‘e’ sigue asombrando a matemáticos, científicos e ingenieros por igual con su belleza y utilidad en la descripción del mundo que nos rodea.